STATISTICS AND PROBABILITY DIPLOMA QUESTION PAPER SOLUTION PART1

 

PROGRAM:

  DIPLOMA IN COMPUTER ENGINEERING  

/ DIPLOMA IN IT

  STATISTICS AND PROBABILITY

MATHEMATICS  

            2 YEAR  // 2 PART

Examples question:

Unit:-4

Pictorial Representation Of a Data Set: – 
Bar Diagrams,Pie(circular,angular) Diagrams ,Histogram And Polygon And Ogive

TYPE 1:          Bar diagram

Question 1:

Get information from your school office about the HSEB result (2018) for the students of Class XII in your school. Draw a bar diagram (showing their aggregate marks classified as 1st division, 2nd division and 3rd division).

ANSWER:

TYPE 2:                 multiple bar diagram

Question 1:

Check your school records on admissions. See how many students were admitted every year during the last 10 years. Classify the data as male and female students. Present the data in the form of a multiple bar diagram.

Year	2003−04	2004−05	2005−06	2006−07	2007−08	2008−09	2009−10	2010−11	2011−12	2012−13
Male Students	40	50	60	45	50	90	65	70	75	80
Female Students	50	30	70	50	50	50	45	80	80	90

ANSWER:

Question 2: 

Make a multiple bar diagram of the following data:
 

Faculty	Number of Students
	2015-16	2016-17	2017-18
Arts Science Commerce	600 400 200	550 500 250	500 600

 Answer:

 

 Number of Students in Different Academic Streams

   TYPE 3:               sub-divided bar diagram

Question 1:

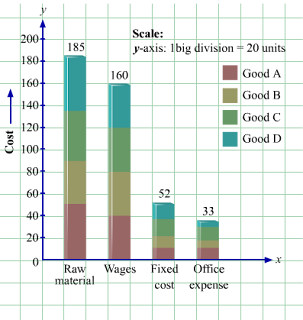
Following table shows estimates of cost of production of certain commodities. Present the data in the form of a sub-divided bar diagram:

Estimate of Cost	Goods
	A	B	C	D
Raw materia Wages Fixed Costs Office expenses	50 40 10 10	40 40 12 8	45 40 15 10	50 40 15 5
Total Cost	110	100	110	110

ANSWER:

Goods
Estimates	A	B	C	D	Total
Raw Materials Wages Fixed Cost Office Expenses	50 40 10 10	40 40 12 8	45 40 15 10	50 40 15 5	185 160 52 33

Question 2:

Present the following data on the production of food grains in the form of a sub-divided bar diagram:
 

Year	Wheat	Rice	Gram	Total
2017 2018	30 45	20 30	10 15	60 90

ANSWER:

Year	Wheat	Rice	Grain	Total
2017	30	20	10	60
2018	45	30	15	90

Type: 4  pie/circular/angular diagram.

Question 1:

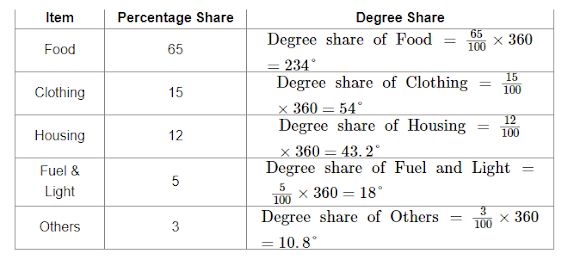
Waht do you mean by a circular diagram? Present the data on the expenditure of a labour-family in the form of a circular diagram:(similar question ask in 2074 shrawan/bhadra Q.12)

Items of Expenditure	Food	Clothing	Housing	Fuel and Light	Others
Percentage of Income Spent	65	15	12	5	3

ANSWER:

Circular diagram or a Pie diagram depicts a circle that is divided into various segments showing the values of different items (components) in percentage terms
For presenting the given percentage values in a pie diagram, the percentage values must be converted into the respective degree values, for which the following formula is used.

                      

Question 2:

For the years 2012-13 and 2013-14, value of gross domestic product at factor cost by the industry of origin is given in the following table. Present the information in the form of Pie Diagram showing differences in the percentage contribution of different sectors between the said years.

  

(similar question ask in 2071 bhadra/Ashwin Q.1)

    

Sector	Year
	2012-13	2013-14
Primary Secondary Tertiary	17 57 26	16.7 26 57.3
Total	100	100

       Answer:

             Type-5  Histogram And Polygon And Ogive

Question 1:

Visit different schools in your locality. Collect information on the daily wage earners. Your information should include (i) daily earnings, and (ii) number of wage earners. Convert the raw data in to a continuous frequency distribution, and present your information in the form a histogram.

Answer:

Daily Earnings	Number of wage earners
0−20 20−40 40−60 60−80 80−100	37 50 70 25 10

Question2:

Construct histogram, frequency polygon and frequency curve from the following data:

For drawing a frequency polygon, we simply join the top mid-points of the rectangles of the histogram drawn above using a straight line.  

Similar to a frequency polygon, for drawing a frequency curve we again joint the top mid-points of the rectangles of the histogram drawn in the first part, but with a free hand 

(rather than a straight line).

Question 3:

Make a  histogram and frequency polygon using the given data:

(similar question ask in 2073/2077/2078-2079 )

Marks Obtained	10−20	20−30	30−40	40−50	50−60	60−70
Number of Students	5	12	15	22	14	4

ANSWER:

For drawing a frequency polygon, we simply join the top mid-points of the rectangle of the histogram as drawn above in the first part using a straight line.

What is meant by ogive or cumulative frequency curve?

👉Ogives or cumulative frequency curve is a smooth distribution curve that depicts cumulative frequency data on a graph paper.

Question 4 (Important)

Graph the following data in the form of 'less than' and 'more than' ogives; and calculate the median value through the graph:  (similar question ask in 2074/2076 )

Marks	0−5	5−10	10−15	15−20	20−25	25−30	30−35	35−40
Number of Students	7	10	20	13	17	10	14	9

ANSWER:

Estimation of the median

Less than and More than Ogive

Marks	Cumulative Frequency
Less than 5 Less than 10 Less than 15 Less than 20 Less than 25 Less than 30 Less than 35 Less than 40	7 7 + 10 = 17 17 + 20 = 37 37 + 13 = 50 50 + 17 = 67 67 + 10 = 77 77 + 14 = 91 91 + 9 = 100

Marks	Cumulative Frequency
More than 0	100
More than 5	100 − 7 = 93
More than 10	93 − 10 = 83
More than 15	83 − 20 = 63
More than 20	63 − 13 = 50
More than 25	50 − 17 = 33
More than 30	33 − 10 = 23
More than 35	23 − 14 = 9
More than 40	9 − 9 = 0

 

So, median is 20.

Question 4

Draw 'less than' and 'more than' ogive curves from the following data:

and compute also median:   (similar question ask in 2074/2076 )

Marks	0−10	10−20	20−30	30−40	40−50
Number of Students	5	10	14	10	3

In order to construct the ogives, we first need to calculate the less than and the more than cumulative frequencies as follows.
 

Marks	Cumulative Frequency
Less than 10 Less than 20 Less than 30 Less than 40 Less than 50	3 3 + 10 = 13 13 + 14 = 27 27 + 10 = 37 37 + 3 = 40

              

Marks	Cumulative Frequency
More than 0 More than 10 More than 20 More than 30 More than 40	40 40 − 3 = 37 37 − 10 = 27 27 − 14 = 13 13 − 10 = 3

The point of intersection of the two types of  ogives curves Gives the median.

i.e, The x co-ordinate of the point of intersection the o gives is the median 

from figure, median=25

Question 4.0:

Draw 'less than' and 'more than' ogive curves from the following data:

         

Marks	0−5	5−10	10−15	15−20	20−25	25−30	30−35	35−40
Number of Students	7	10	20	13	12	19	14	9

ANSWER:

(i) For constructing a less than ogive, first the given frequency distribution must be converted into a less than cumulative frequency distribution as follows. 

Marks	Cumulative Frequency
Less than 5 Less than 10 Less than 15 Less than 20 Less than 25 Less than 30 Less than 35 Less than 40	7 7 + 10 = 17 17 + 20 = 37 37 + 13 = 50 50 + 12 = 62 62 + 19 = 81 81 + 14 = 95 95 + 9 = 104

We now plot the cumulative frequencies against the upper limit of the class intervals. The curve obtained on joining the points so plotted is known as the less than ogive.

(ii) For constructing a less than ogive, first the given frequency distribution is converted into a more than cumulative frequency distribution as follows. ​

Marks	Cumulative Frequency
More than 0	104
More than 5	104 − 7 = 97
More than 10	97 − 10 = 87
More than 15	87 − 20 = 67
More than 20	67 − 13 = 54
More than 25	54 − 12 = 42
More than 30	42 − 19 = 23
More than 35	23 − 14 = 9
More than 40	9 − 9 = 0

We now plot the cumulative frequencies against the lower limit of the class intervals. The curve obtained on joining the points so plotted is known as the more than ogive.

Question 5:

Represent the following data in the form of a histogram:

Mid-point	115	125	135	145	155	165	175	185	195
Size	6	55	48	72	116	60	38	22	3

👉 

In order to construct a histogram, we first require the class intervals corresponding to the various mid-points, which is calculated using the following formula.

 

The value obtained is then added to the mid point to obtain the upper limit and subtracted from the mid-point to obtain the lower limit.

For the given data, the class interval is calculated by the following value of adjustment.
Value of Adjustment = 125 −115 2 = 5$\mathrm{Value} \mathrm{of} \mathrm{Adjustment} = \frac{125 -115 }{2} = 5$

Thus, we add and subtract 5 to each mid-point to obtain the class interval.

For instance:

The lower limit of first class = 115 – 5 = 110

Upper limit of first class = 115 + 5 = 120.

Thus, the first class interval is (110-120). Similarly, we can calculate the remaining class intervals.

Mid Point	Class Interval	Size
115	110 − 120	6
125	120 − 130	55
135	130 − 140	48
145	140 − 150	72
155	150 − 160	116
165	160 − 170	60
175	170 − 180	38
185	180 − 190	22
195	190 − 200	3

Question 10:

The frequency distribution of marks obtained by students in a class test is given below. Draw frequency polygon(without histogram) 

Marks	0−10	10−20	20−30	30−40	40−50
Number of Students	5	10	14	10	3

👉 In order to construct a frequency polygon without a histogram, we first calculate the mid-points corresponding to the class intervals. The mid-points are then plotted against their respective frequencies. The curve obtained on joining the points is the frequency polygon.

Question 11:(Importance)

Draw 'less than' as well as 'more than' ogives for the following data:

Weight (in Kg)	30−34	35−39	40−44	45−49	50−54	55−59	60−64
Frequency	3	5	12	18	14	6	2

Before proceeding to construct the ogives, we first need to convert the given inclusive series into an exclusive series using the following formula. 

The value of adjustment as calculated is then added to the upper limit of each class and subtracted from the lower limit of each class.
Here, the value of adjustment = 35 − 342 = 0.5

Therefore, we add 0.5 to the upper limit and subtract 0.5 from the lower limit of each class.

Weight	Frequency
29.5 − 34.5 34.5 − 39.5 39.5 − 44.5 44.5 − 49.5 49.5 − 54.5 54.5 − 59.5 59.5 − 64.5	3 5 12 18 14 6 2

Now for constructing a less than ogive, we convert the frequency distribution into a less than cumulative frequency distribution as follows. 

Weight	Cumulative Frequency
Less than 34.5 Less than 39.5 Less than 44.5 Less than 49.5 Less than 54.5 Less than 59.5 Less than 64.5	3 3 + 5 = 8 8 + 12 = 20 20 + 18 = 38 38 + 14 = 52 52 + 6 = 58 58 + 2 = 60

We now plot the cumulative frequencies against the upper limit of the class intervals. The curve obtained on joining the points so plotted is known as the less than ogive.

For constructing a more than ogive, we convert the frequency distribution into a more than cumulative frequency distribution as follows.

Weight	Cumulative Frequency
More than 0 More than 34.5 More than 39.5 More than 44.5 More than 49.5 More than 54.5 More than 59.5 More than 64.5	60 60 − 3 = 57 57 − 5 = 52 52 − 12 = 40 40 − 18 = 22 22 − 14 = 8 8 − 6 = 2 2 − 2 = 0

We now plot the cumulative frequencies against the lower limit of the class intervals. The curve obtained on joining the points so plotted is known as the more than ogive.

unit 5:

SUMMARIZING A DATA SET:

👉CENTERAL TENDENCY(MEAN,MEDIAN,MODE)

👉VARIABILITY OF DISPERSION(RANGE,INTER-QUARTILE RANGE,QUARTILE DEVIATION, QUARTILE,PERCENTILE,DECILE ,STANDARD DEVIATION,COFFICIENT OF VARIATION)

Question 1:

Calculate mode of the following series:

(similar question ask in 2077)

Class Interval	0−5	5−10	10−15	15−20	20−25	25−30
Frequency	20	24	32	28	20	26

Class Interval	Frequency
0 − 5 5 − 10 (l₁)10 − 15 15 − 20 20 − 25 25 − 30	20     24 f0     32 f1     28 f2 20 26

Question 2:

Estimate quartile deviation

(similar question ask in 2073)

 and the coefficient of quartile deviation of the following data:
8, 9, 11, 12, 13, 17, 20, 21, 23, 25, 27
Show that QD is the average of the difference between two quartiles

Sr. No.	1	2	3	4	5	6	7	8	9	10	11
Data	8	9	11	12	13	17	20	21	23	25	27

In order to find the quartile deviation in case of individual series, find out the values of  first quartile and third quartile using the following equations:

Q1 = Size of (N+14)thitem
or,  Q1     = Size of (11+14)th item
or,  Q1     = Size of 3rd item
⇒$\Rightarrow$  Q1     = 11

Q3 = Size of 3(N+14)th item

or,  Q3  = Size of 3(11+14)th item
or,   Q3 = Size of 9th item
⇒$\Rightarrow$    Q3 = 23

Question 2:
(similar question ask in 2078-79)

Find out mean deviation and its coefficient of the following data:

Items	5	10	15	20	25	30	35	40
Frequency	8	16	18	22	14	9	6	7

ANSWER:

Items (X)	Frequency (f)	fX	Deviation from Mean ∣X−x̄∣= ∣dX∣		f∣dX∣
5	8	40	15.2	121.6
10	16	160	10.2	163.2
15	18	270	5.2	93.6
20	22	440	0.2	4.4
25	14	350	4.8	67.2
30	9	270	9.8	88.2
35	6	210	14.8	88.8
40	7	280	19.8	138.6
	Σf = 100	Σfx = 2020		Σf∣dX∣=765.6

a) Mean (X¯¯¯)=ΣfxΣf=2020100=20.2

(b) Mean deviation from Arithmetic Mean

MDX=Σf∣∣dX∣∣Σf=765.6100=7.656

(c) Coefficient of MDX¯¯¯${\stackrel{}{\mathit{¯}}}_{}$ =MDXX=7.65620.2=0.379=0.38 approx.
MDX¯¯¯M=]
MDXX=7.65620.2=0.379=0.38 approx.

Question 3:

(similar question ask in 2077 Q.12)

Find the mean deviation from mode 

Value	20-30	30-40	40-50	50-60	60-70
Frequency	8	24	42	20	6

ANSWER:

A glance at the series reveal that 40 − 45 is the modal class because it has the maximum frequency i.e. 42. Therefore ,the modal value will be:

Coefficient of Variation

Standard variation is an absolute measure of dispersion. When comparison has to be made between two series then the relative measure of dispersion, known as coeff.of variation is used.

Coefficient of Variation, CV is defined and given by the following function:

CV=σX×100

Where 

• $CV$ = Coefficient of Variation.

• $\sigma$ = standard deviation.

• 
  $X$ = mean.

• 
  

• Comparison of C.V. of two data:

• Let assumed   (C.V)₁   and (C.V)₂

• 👉 Less the C.V.,more will be uniformity, consistency,etc.

• 👉more the C.V., Less will be uniformity, consistency,etc.

• 👉The lower the value of the coefficient of variation, the more precise the estimate.

• 👉more the C.V., More will be variability, 

• 👉  Example:An analysis of monthly wages paid to the workers in two firm belonging to the same industry 

                                                                Firm A                                       Firm B

  No. of workers:                                  600                                     700

  Average monthly wage:                   Rs182.00                       Rs178.50

   Variance of distribution of wage:  78                                98    

  i)                 Which firm A or B has a larger wage bill?

  ii)  In which firm A or B is there greater variability in individual wages ?

• give the following results:

•  ANSWER:

• 
  
  

  (i) From the above results, form B has a larger wage bill.

  (ii)Since the C.V. for firm B is greater than that of A, so the distribution of wages

•  in firm B has greater variability.

(i) From the above results, form B has a larger wage bill.

(ii)Since the C.V. for firm B is greater than that of A, so the distribution of wages in firm B has greater variability.

  

STATISTICS AND PROBABILITY   DIPLOMA  SYLLABUS HINT QUESTION

NEW PAST QUESTION FROM(2079-2070) SOLVED

I) from bivariate frequency Find Coefficient of corelation.

II) FINDING GEOMETRIC MEAN AND HARMONIC MEANS:

PROBABILITY

# concept of probability

i)Binomial distribution

ii) Random variable

iii) Possion distribution

LINK HERE

 STATISTICS

 AND PROBABILITY

QUESTION COLLECTION

                       

   PDF LINK:  2076

                           2077 

                         2079

       More added Soon.....